YouTubeチャンネル:微積で高校物理~大学受験に向けて~の運営者
微積物理の基礎
加速度・速度・位置の関係は微分積分で定義されている
まずは加速度・速度・位置の関係を学びましょう。
加速度を\(a(t)\)、速度を\(v(t)\)、位置を\(x(t)\)とすると、これらの間にはどのような関係があるかだろうか?
実はこれらの関係は以下のように定義される

数式で書けば加速度\(a(t)\)は\(v(t)\)を1回微分または\(x(t)\)を2回微分したものである。
すなわち、
\[\begin{eqnarray}
a(t)&=&\frac{dv(t)}{dt}=\dot{v}(t) \\
&=&\frac{d^{2}x(t)}{dt^{2}}=\ddot{x}(t)
\end{eqnarray}\]
※\(\dot{v}(t)\)はニュートン記法と言い、\(v(t)\)をtで1回微分したものという意味。「vドット」と読む。
また、\(\ddot{x}(t)\)は\(x(t)\)をtで2回微分したものという意味。「xツードット」と読む。
速度\(v(t)\)は\(x(t)\)を1回微分したものである。
すなわち、
\[v(t)=\frac{dx(t)}{dt}=\dot{x}(t)\]
簡単な例について一緒に考えてみよう
自由落下
上図のように\(y\)軸を上向きにとり、\(y=h\)から物体を静かに離した。ただし、重力加速度は\(y\)軸負方向に大きさ\(g\)だとする。このときの運動を考えてみよう。
まず、加速度\(\ddot{y}(t)\)は下記のようになる。
\begin{equation} \tag{1}\label{ddoty1}
\ddot{y}(t)=-g
\end{equation}
\eqref{ddoty1}を\(t\)で1回積分すれば速度\(\dot{y}(t)\)が下記のように求まる。この際の積分定数は、\(\dot{y}(0)=0\)なので\(0\)である。
\begin{equation}\tag{2}\label{doty1}
\dot{y}(t)=-gt
\end{equation}
さらに、\eqref{doty1}を\(t\)で積分すれば位置が求まる。この際の積分定数は\(y(0)=h\)なので\(h\)である。
\begin{equation}\tag{3}\label{y1}
y(t)=-\frac{1}{2}gt^{2}+h
\end{equation}
以上で問題を解く準備は完了!加速度を求めてあげて\(t\)で2回積分してあげるだけなので超簡単ですよね!教科書に載っている公式を覚える必要は全くございません。では、具体的に良く聞かれる問題を一緒に考えてみましょう。
地面\(y=0\)に落下するまでの時間\(t_{1}\)は?という設問があったとします。みなさんならどう解きますか?この場合は、素直に\eqref{y1}より\(y(t_{1})=0\)を解いてあげればOKです。
すなわち
\[y(t_{1})=-\frac{1}{2}gt_{1}^{2}+h=0\]
\[\therefore\ t_{1}=\sqrt{\frac{2h}{g}}\]
と\(t_{1}\)が求まります。いかがですか?超簡単じゃないですか?
続きまして、地面に到達した瞬間の速度を求めてみましょう。これは\eqref{doty1}に\(t=t_{1}\)を代入すればOKですね。
すなわち、
\begin{eqnarray}
\dot{y}(t_{1})&=&-gt_{1} \\
&=&-g\sqrt{\frac{2h}{g}} \\
&=&-\sqrt{2gh}
\end{eqnarray}
と求まるわけです。いかがでしょうか?最初の準備さえできてしまえばあとはただの計算問題でしたね!
鉛直投げ上げ
続きまして「鉛直投げ上げ」を一緒に考えてみましょう。下図のように初速\(v_{o}\)で\(y\)軸正方向に投げ上げを行ったとすると加速度\(\ddot{y}\)、速度\(\dot{y}\)、位置\(y\)は同様に
\begin{equation} \tag{4}\label{ddoty2}
\ddot{y}(t)=-g
\end{equation}
\(\dot{y}(0)=v_{o}\)であることに注意して、加速度\(\ddot{y}\)を\(t\)で積分して
\begin{equation} \tag{5}\label{doty2}
\dot{y}(t)=-gt+v_{o}
\end{equation}
\(y(0)=0\)であることに注意して、速度\(\dot{y}\)を\(t\)で積分して
\begin{equation} \tag{6}\label{y2}
y(t)=-\frac{1}{2}gt^{2}+v_{o}t
\end{equation}
が得られる。
例えば、\(y=h\)に到達する時刻\(t=t_{2}\)を問われたとしよう。この場合には、\(y=h\)で速度がゼロになるため、\eqref{doty2}より\(\dot{y}(t_{2})=0\)を解いてあげればよい。これを解くと、
\[t_{2}=\frac{v{o}}{g}\]
と求まる。さらに\(h\)は?と問われたとしたら、\eqref{y2}に\(t=t_{2}\)を代入して、\(h=y(t_{2})\)を求めてあげればよい。すなわち、
\begin{eqnarray}
h&=&y(t_{2}) \\
&=&-\frac{1}{2}gt_{2}^{2}+v_{o}t_{2} \\
&=&\frac{v_{o}^{2}}{2g}
\end{eqnarray}
と求まる。このようにして加速度さえわかってしまえばシステマティックに解答できるわけである。
モンキーハンティング
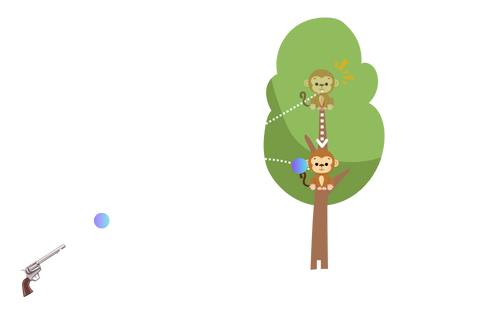
最後にめちゃめちゃ有名なモンキーハンティングの問題を一緒に解きましょう!モンキーハンティング問題をご存じない方もいるかもしれませんので説明します。木の上\((x,y)=(l,h)\)の座標にいるサルに向けて原点から初速\(v_{o}\)で銃弾を発射します。木の上にいるサルはその銃声に驚いて、銃声と同時に木から落っこちます。このとき、木から「自由落下」したサルに銃弾が命中する条件を求めるという問題がモンキーハンティングです。
さて、上記と同様に加速度を積分して銃弾とサルの速度・位置を求めていきましょう!
銃弾
まず、加速度は
\begin{equation}
\ddot{x}(t)=0 \\
\ddot{y}(t)=-g
\end{equation}
これを\(t\)で1回積分することによって下記のように速度の式が得られる。
※この際、\(\dot{x}(0)=v_{o}cos\theta \)、\(\dot{y}(0)=v_{o}sin\theta \)が積分定数になることに注意
\begin{equation} \tag{7}\label{dotxtama}
\dot{x}(t)=v_{o}cos\theta
\end{equation}
\begin{equation} \tag{8}\label{dotytama}
\dot{y}(t)=-gt+v_{o}sin\theta
\end{equation}
さらに、速度の式を\(t\)でもう一度積分することによって下記のように位置が求まる
※この際、\(x(0)=0 \)、\(y(0)=0 \)が積分定数になることに注意
\begin{equation} \tag{9}\label{xtama}
x(t)=v_{o}cos\theta\ t
\end{equation}
\begin{equation} \tag{10}\label{ytama}
y(t)=-\frac{1}{2}gt^{2}+v_{o}sin\theta\ t
\end{equation}
これで銃弾の速度および位置の式を求めることができました!
次にサルの速度および位置の式を求めていきましょう。
サル
サルの加速度は
\begin{equation}
\ddot{X}(t)=0 \\
\ddot{Y}(t)=-g
\end{equation}
初期条件(積分定数になる)に注意して1回積分すると速度が求まる。
\begin{equation} \tag{11}\label{dotxsaru}
\dot{X}(t)=0
\end{equation}
\begin{equation} \tag{12}\label{dotysaru}
\dot{Y}(t)=-gt
\end{equation}
初期条件(積分定数になる)に注意してもう1回積分すると位置が求まる。
\begin{equation} \tag{13}\label{xsaru}
X(t)=l
\end{equation}
\begin{equation} \tag{14}\label{ysaru}
Y(t)=-\frac{1}{2}gt^{2}+h
\end{equation}
このようにして、サルの速度と位置もtの式で表すことができました!
では、よく問われる問題を解いていきましょう。
①銃弾が木\((x=l)\)に到達する時刻\(t_{1}\)は?
この場合には\eqref{xtama}に\(t=t_{1}\)を代入してあげればよいでしょう。
つまり、
\[x(t_{1})=v_{o}cos\theta\ t_{1}=l\]
より
\[t_{1}=\frac{l}{v_{o}cos\theta}\]
となります。
②銃弾がサルに命中するとき\(tan\theta\)の条件は?
もし銃弾がサルに命中するならば、
\[y(t_{1})=Y(t_{1})\]
が成り立つので、\eqref{ytama}と\eqref{ysaru}より
\[-\frac{1}{2}gt_{1}^{2}+v_{o}sin\theta\ t_{1}=-\frac{1}{2}gt_{1}^{2}+h\]
これに①で求めた\(t_{1}\)を代入して\(tan\theta\)を求めると
\[tan\theta=\frac{h}{l}\]
と求まる。この式は、発射前にサルに銃口を向けておかなれければならないということを(照準を合わせておく)意味している。
③サルが地面に落下する前に銃弾が命中する\(v_{o}\)の条件は?
この条件は\(Y(t_{1})>0\)ですね!
したがって、
\[Y(t_{1})=-\frac{1}{2}gt_{1}^{2}+h>0\]
より
\[-\frac{1}{2}g\Bigl(\frac{l}{v_{o}cos\theta}\Bigr)^{2}+h>0\]
であるから、\(v_{o}\)について整理すると
\[v_{o}>\sqrt{\frac{1}{2}\frac{gl^{2}}{h}\frac{1}{cos^{2}\theta}}=\sqrt{\frac{1}{2}\frac{gl^{2}}{h}(1+tan^{2}\theta)}=\sqrt{\frac{1}{2}\frac{gl^{2}}{h}\Bigl(1+\frac{h^{2}}{l^{2}}\Bigr)}\]
\[\therefore\ v_{o}>\sqrt{\frac{g}{2h}(l^{2}+h^{2})}\]
と求めることが出来ます。
ここまでいかがでしたか?おそらく多くの方にいわゆる「微積物理」を楽しんでいただけたと思っています!
もし何かわからないことがあればコメントお願いします。
おすすめ参考書&問題集
問題集
良問の風:私のYouTubeチャンネルで微積物理の詳解が見れます
名問の森:良問の風よりも少しだけハイレベルな問題を扱っています。私のYouTubeチャンネルで微積物理の詳解が見れます
参考書
「新・物理入門〈増補改訂版〉 (駿台受験シリーズ)」
”微積物理”のバイブルです。これと私のチャンネルの動画を組み合わせると最強です。
理論物理への道標:新物理入門よりもとっつきやすいと思います。両方ご購入いただきまずはこちらから読んでみるのがおすすめです!










コメント